Contact: Prof. Gennady El

• Dr. Costanza Benassi
• Dr. Thibault Congy
• Dr. Remy Dubertrand
• Prof. Gennady El
• Dr. Benoit Huard
• Dr. Yiping Ma
• Dr. Antonio Moro
• Dr. Daniel Ratliff
• Prof. Emiliano Renzi
• Dr. Giacomo Roberti
• Dr. Matteo Sommacal

Postdocs

• Dr Dmitry Agafontsev

Visiting scholars

• Prof. Mark Hoefer

Postgraduate researchers

• Michael Armstrong
• Henry Carr
• David Martin

Newton Institute satellite programme: Emergent phenomena in nonlinear dispersive waves (for details https://www.newton.ac.uk/event/pdw/)

The group is part of the organising committee of a month-long thematic programme on Emergent phenomena in nonlinear dispersive waves to be held at Northumbria and Newcastle Universities, 22 July - 16 August 2024.

Mathematics of delayed phenomena: Theory, applications and numerics

A two-day workshop on the dynamics of time-delay systems at Northumbria. 22-23 March 2023. Supported by the London Mathematical Society. For more details: https://sites.google.com/view/mdp2023/home.

Newton Institute: Dispersive Hydrodynamics (see press release here)

The group is part of the organising committee of a 6-month programme on Dispersive hydrodynamics: mathematics, simulation and experiments, with applications in nonlinear waves to be held at the Newton Institute in Cambridge, 4 July - 16 December 2022.
The scientific program is organised around four themes:

• Modulation theory and dispersive shock waves
• Analysis of dispersive systems
• Statistical mechanics, integrability and dispersive hydrodynamics
• Physical applications

For more details: https://www.newton.ac.uk/event/hyd

New horizons in dispersive hydrodynamics

Virtual bridging workshop aims at exploring novel, cross-disciplinary connections of dispersive hydrodynamics within the four main themes of the above forthcoming 6-month programme at the Newton Institute. Will be held 21st June to 2nd July 2021.
Details at https://www.newton.ac.uk/event/hydw08.

4th IMA Conference on Nonlinearity and Coherent Structures

Online conference on nonlinearity in applied Mathematics, mathematical Analysis, fluid dynamics, engineering and physics. To be held 7 - 9 July 2021.
Details at https://ima.org.uk/15373/4th-ima-conference-on-nonlinearity-and-coherent-structures/.

Seminars take place at 3pm in room ELA002 (Ellison building, 9a on campus map).

The seminar schedule can be found here.

Contact for more information

Antonio Moro: antonio.moro(AT)northumbria.ac.uk

Dispersive hydrodynamics

Dispersive hydrodynamics has emerged as a unified mathematical framework for the description of multiscale nonlinear wave phenomena in dispersive media, encompassing both dynamic and stochastic aspects of wave propagation. Recent theoretical and experimental developments have opened up new areas for research, with intriguing open issues in both theory and applications. These include the understanding of fundamental regularisation mechanisms of hydrodynamic singularities via the generation of dispersive shock waves (DSWs) and related phenomena. Physical examples of dispersive hydrodynamic phenomena include undular bores on rivers, in the ocean and atmosphere, nonlinear diffraction patterns in optics and quantum fluids, turbulence in fibre lasers and superfluids.

The dispersive hydrodynamics research in the MCNP group is centred around four major themes:

• Dispersive shock waves in integrable and non-integrable systems
• Integrable turbulence and soliton gas
• Extreme nonlinear wave phenomena
• Physical applications in fluid mechanics and nonlinear optics

The mathematics employed involve a synthesis of exact and asymptotic methods from soliton theory, hyperbolic conservation laws and Whitham modulation theory. The analytical developments are supported by careful numerical simulations and, when possible, comparisons with available experimental and observational data.

Lead by: Gennady El

Key publications:

• G. A. El and A. Tovbis, arXiv:1910.05732 (2019)
• M. D. Maiden, D. V. Anderson, N. A. Franco, G. A. El, and M. A. Hoefer, Phys. Rev. Lett. 120, 144101 (2018)
• G. A. El and M. A. Hoefer, Physica D 33, 11-65 (2016)
• G. A. El, E. G. Khamis, and A. Tovbis, Nonlinearity 29, 2798-2836 (2016)

Funding: EPSRC (2017-2010, Grant No. EP/R00515X/1); Dstl (2017-2020, Contract No DSTLX-1000116851); LumOptica (2019-2020, Contract Research Grant), the London Mathematical Society Research in Pairs Grants (2014, 2015, 2017, 2018, 2019), the Royal Society International Exchanges Scheme (2014-2016).

Integrability and Complexity

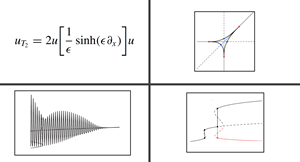
Integrability and Complexity are often viewed as antinomic concepts. The notion of Integrability is associated to systems that exhibit some form of regularity and therefore are "simple enough" to be solved analytically. The idea of Complexity arises in a variety of contexts where a system shows features such as chaos, disorder, instability, randomness.

The modern theory of integrable systems demonstrates that it is indeed possible to use analytical techniques to capture and describe complex behaviours in nonlinear and many-body systems. The research focuses on the method of differential identities as a unified approach to the solution of a general class of statistical mechanical systems, from classical "simple" systems, which exhibit Ising type phase transitions, to systems where complex behaviours emerge. Key features of a variety statistical mechanical models, e.g. critical and collective behaviours, scaling properties, can be understood and explained in terms of scaling properties and regularisation mechanisms of singularities of nonlinear integrable systems. Main research topics are:

• Partition functions of statistical mechanical systems, random graph and random matrix models.
• Singular limits of nonlinear integrable partial differential equations and multiscale asymptotics.
• Classical and dispersive shocks of order parameters.
• Classification of nonlinear integrable partial differential equations and normal forms.

Lead by: Antonio Moro

Key publications:

• C. Benassi and A. Moro, Phys. Rev. E 101, 052118 (2020)
• G. De Matteis, F. Giglio, and A. Moro, Annals of Physics 396 386-396 (2018)
• B. Dubrovin, T. Grava, C. Klein, and A. Moro, J. Nonlinear Sci., 25 631-707 (2015)
• A. Moro, Annals of Physics. 343 49-60 (2014)

Funding: Leverhulme Trust Research Project Grant (2018-2021, PI: A. Moro; Grant Ref. RPG-2017-228) - Dressing methods and complexity reduction for integrable networks models; Royal Society International Exchanges (2017-2019) - PI: A. Moro; Co-I: G. Biondini - p-Stars and KP: soliton phase diagrams for complex systems.

Classical-to-quantum correspondence for many-body systems

This research aims to understand the transition from a classical system to its quantum analogue. This fundamental research domain, sometimes dubbed 'quantum chaos', has had numerous connections ranging from physics (nuclear physics, microwave cavities, transport in quantum dots) to mathematics (number theory, spectral theory, dynamical systems). In the physics community, there has been recently a renewed attention to apply these techniques for quantum systems composed of interacting particles, under the name of 'many-body quantum chaos'. I am interested in the more fundamental questions, which are raised when studying a quantum many-body system/model using a semiclassical perspective.

Lead by: Rémy Dubertrand

Key publications:

• R. Dubertrand and S. Müller, New J. Phys. 18, 033009 (2016)
• I. García-Mata, O. Giraud, B. Georgeot, J. Martin, R. Dubertrand, and G. Lemarié, Phys. Rev. Lett. 118, 166801 (2017)

Metamaterials and geophysics dynamics

• Nonlinear waves in optical and mechanical topological insulators
• Localized pattern formation in driven dissipative systems
• Mathematical models of meltwater features in cold environments

Lead by: Yiping Ma

Key publications:

• D. D. J. M. Snee and Y.-P. Ma, Ext. Mech. Lett. 30, 100487 (2019)
• Y.-P. Ma, I. Sudakov, C. Strong, and K. M. Golden, New J. Phys. 21, 1367-2630 (2019)
• Y.-P. Ma and E. Knobloch, Physica D 337, 1-17 (2016)

Modulation of nonlinear waves and dispersive shock waves

The Whitham modulation theory describes intermediate and long-time dispersive hydrodynamics, and has proved particularly effective in the determination of nonlinear waves such as the celebrated dispersive shock wave (DSW) solution. My research explores new developments and applications of the modulation theory, with the description of:

• DSWs in non-integrable systems (e.g. Serre fully nonlinear shallow water equations)
• New wave structures in systems with nonconvex dispersion (e.g. Benjamin-Bona-Mahony equation)
• Interactions between nonlinear waves within the framework of wave-mean flow interaction

Lead by: Thibault Congy

Key publications:

• T. Congy, G. A. El, and M. A. Hoefer, J. Fluid Mech. 875, 1145-1174 (2019)
• T. Congy, G. A. El, M. A. Hoefer, and M. Shearer, Stud. Appl. Math. 142, 241-268 (2019)
• S. K. Ivanov, A. M. Kamchatnov, T. Congy, and N. Pavloff, Phys. Rev. E 96, 062202 (2017)

Nonlinear dynamics in delayed feedback systems

Cyclic rhythms are crucial for the proper functioning and robustness of many biological systems. These are often described using nonlinear differential equations which incorporate feedback mechanisms with inherent delays of various types. The characterisation of periodic solutions in such systems provides markers of accuracy for these rhythms as well as pathways for restoring them. A particular emphasis given to the glucose-insulin regulation system.

Lead by: Benoit Huard

Key publications:

• A. Bridgewater, B. Huard, and M. Angelova, J. Nonlinear Sci. 30, 737-766 (2020)
• B. Huard, A. Bridgewater, and M. Angelova, J. Theor. Biol. 418, 66 - 76 (2017)
• B. Huard, M. Angelova, and J. Easton, Commun. Nonlinear Sci. 26, 211 - 222 (2015)

Funding: Newton Advanced fellowship from the British Academy of Sciences.

Nonlinear waves and complex dynamics

• Nonlinear waves in ferromagnetic systems: Localised, propagating magnetic structures in 1- and 2-dimensional ferromagnetic systems at the nanometre length-scale. Classical, continuous Heisenberg ferromagnet equation. Landau-Lifshitz equation with uni-axial and bi-axial anisotropy.
• Integrability and linear stability of nonlinear waves: Linear stability analysis of scalar and multi-component, nonlinear partial differential equations of integrable type. Manakov system. Vector nonlinear Schrödinger equation. Three waves resonant interaction equation.
• Complex dynamics and Riemann surfaces: Understanding complex dynamics by means of an associated Riemann surface. Circular flow on a compact Riemann surface. Landen transformations. Slow chaos and parabolic dynamical systems.

Lead by: Matteo Sommacal

Funding: LMS, Research in Pairs - Scheme 4, "Instabilities of nonlinear waves by means of elementary algebraic-geometry", Grant Ref. 41808 (2019). LMS, Research in Pairs - Scheme 4, "Propagating, localised waves in ferromagnetic nanowires", Grant Ref. 41622 (2017).

Phase transitions in spin systems and random matrix models

Statistical mechanics is the field of mathematical physics describing the collective behaviour of macroscopic systems from the aggregated features of their microscopic components. A typical phenomenon observed in this context in various physical models is phase transitions, an abrupt change in the qualitative features of the system when its parameters (e.g. temperature, magnetic field) are tuned. In my research I focus on the investigation of phase transitions in various models, specifically lattice spin systems and random matrix models. Lattice spin systems provide a simplified description of the magnetic behaviour of solid materials, and some of them can be investigated using their relationship with a class of probabilistic models describing interacting random loops. Random matrix models present very distinctive phase transitions, and can be explored exploiting their underlying integrable structure and the tools provided by dispersive hydrodynamics.

Lead by: Costanza Benassi

Key publications:

• C. Benassi and A. Moro, Phys. Rev. E 101, 052118 (2020)
• C. Benassi and D.Ueltschi, Commun. Math. Phys. doi:10.1007/s00220-019-03474-9 (2019)
• C. Benassi, J. Fröhlich, and D. Ueltschi, Ann. Henri Poincaré 18, 2831-2847 (2017)

This group is a part of the University’s multi-disciplinary research into the theme of Extreme Environments.

To view research papers emanating from this group, please click here to view Northumbria Research Link, our open access repository of research output from Northumbria University.